If is the execution time of task and is its request period, then the processor utilization is defined as the fraction of time during which the processor is busy running one of the tasks and is given as .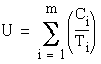

Corresponding to the priority assignment of a set of tasks, it is said that these tasks fully utilize the processor if the priority assignment is feasible and an increase in the run time of any of the tasks in the set will make the priority assignment infeasible.

For a given fixed priority scheduling algorithm, the least upper bound of the utilization factor is the minimum of the utilization factors over all sets of tasks that fully utilize the processor. This means that for all task sets whose utilization factor is below this bound, there exists a priority assignment that is feasible.

On the other hand any task set with utilization factor greater than this bound can only achieve a feasible schedule if the task periods and execution times are specially related to each other.

Since the rate monotonic scheduling is optimum, it means that the utilization factor achievable under such a scheduling, will be greater than or equal to the utilization factor achievable by other schedules.

Thus the least upper bound is the minimum of the utilization factors obtained by the rate-monotonic scheduling.

The previous discussion and examples focused mainly on sets of two tasks. In case of more than two tasks, the calculus becomes more involved. Equation (2.8) must be used which includes the nonlinear functions .

In the subsequent, we shall establish a simple method of determining whether a set of tasks can be feasibly scheduled. Our approach will establish a lower bound on the utilization factor for tasks that fully utilize the processor. Any set of tasks that have a utilization factor that is lower than the bound, as we shall see, can be feasibly scheduled.

Theorem 2.3: For a set of two tasks with fixed priority assignments, the least upper bound to the processor utilization factor is U = 2(2 1/2-1). Proof

Theorem 2.4.For a set of m tasks with fixed priority and the restriction that the ratio between any two request periods is less than 2, the least upper bound of the processor utilization factor is . Proof
Theorem 2.5.For a set of m tasks with fixed priority order, the least upper bound of the processor utilization is given as . Proof

Theorem 2.6. Any set of m tasks with a utilization factor is feasible. Proof