3.2.2 Calculating the l.u.b of the processor utilization for the Deferrable Server
Theorem
3.3: For a set of m fixed priority tasks 
with 
where 
is the deferrable server, the least upper bound of the utilization
function is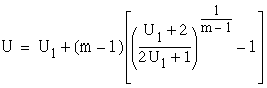 
.
Proof
3.2.3 Special Case
This case presumes that all the tasks have approximately
equal periods with a variation within 
. As we shall demonstrate,
this arrangement results in a very low least upper bound of the utilization
factor. For such a set of tasks, their repetition periods observe the
following relation. 
In this case, all the periodic tasks must execute within
and 
as depicted in Figure 3.6 below.
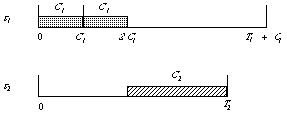
Figure 3.6: Worst case task arrangement.
Let's assume the case of two tasks and remember that we are seeking the absolutely worst scenario.
The utilization factor for this case is calculated as follows:
then,
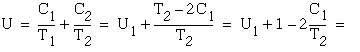
Assuming 
(this guarantees that there would always exist time for C2 to execute,
as we shall see subsequently) and since 
the absolutely possibly worst case, is when 
or 
. Then the lower bound of the utilization is given as 
.
In case that 
, then the absolutely worst situation is when 
does not have enough time
to execute. This can be seen as follows: Suppose that 
, then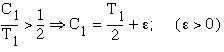 
.
One can always find T2 such that
.
This period is within the postulated assumptions i.e.
T2 > T1 (since 
> 0) and 
But for any such period, 
; thus 
does not have enough time to run.
The utilization factor then is given as 
Plotting the utilization factor U in terms of 
, one gets
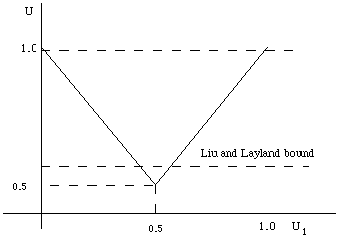
Figure 3.7: The least upper bound of the utilization factor of the deferrable server where the periods of all the tasks are approximately equal.
The analysis outlined above for two tasks can be generalized
for m tasks as follows: If 
, then tasks 
must execute within 
and 
.
Thus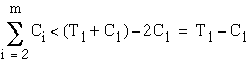 
Consider now a new aggregate task 
with 
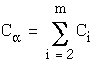and 
.
Since 
then
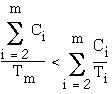
Thus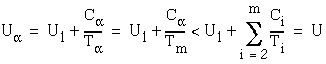 
Therefore, for any set of m tasks, we can always construct
a set of two tasks which has a utilization factor 
that is always less than the utilization factor U of the set of m tasks.
Thus, the least upper bound of the utilization factor for the m tasks
is exactly that of the case of two tasks as discussed earlier.
3.2.4 Experimental Results
The two policies together with standard polling and aperiodic-tasks-in-the-background were simulated to study the sensitivity of the response times to the length of the period of the periodic server.
The aperiodic tasks were assumed to be Poisson distributed
with constant mean inter-arrival time (
) and mean run time (r). The server task and periodic task environments
were chosen so that the periodic load component was 0.45 and the utilization
of the periodic server was computed from equations (3.5) (Priority Exchange)
and (3.14) (Deferrable Server).
Denoting by PLPE and PLDS the processor utilization due to the periodic tasks for the Priority Exchange and Deferrable Server cases respectively, we have from (3.5) and (3.14).
and 
. Then
and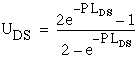 
.
Setting 
, then 
and 
.
The simulations used 
and 
for the utilization factors of the periodic servers. The results appear
in Figure 3.8.
The response time for the polling server increases as the period of the server increases, and this is expected since the interval between server invocations increases, and thus arriving aperiodic tasks have to wait longer on the average before they are serviced.
For the Priority Exchange and Deferrable Servers, the response time decreases as the period of the server increases, indicating their ability to respond as soon as aperiodic tasks arrive. Observe though that as the period of the server increases, its priority decreases (according to the rate monotonic assignment that governs the periodic environment). Thus, for large periods which correspond to the lowest priority, the response time becomes identical to that of the aperiodic-tasks-in-the-background discipline.
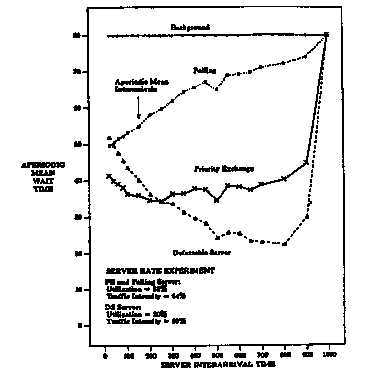
Figure 3.8: The sensitivity of the response time of the aperiodic tasks on the length of the period of the periodic server. (from [5]).