2.1 Fixed Priority Scheduling (Rate Monotonic Scheduling)

Denote by m tasks, by ; i =1, 2, ... m their request periods and by i=1, 2, ... m their execution times.

Define as r_i the response time for a task t_i as the time span between its request and the end of the response to the request. Note that during the response time of a task, no lower priority tasks can execute and that the deadline of a task coincides with the end of its period

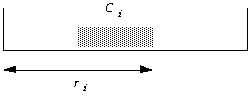
Figure 2.1: A periodic task, its run and response times.

Define as the critical instant for a task t _i as the instant at which the request for this task would have the largest response time.

Define as a critical time zone for a task the response time of a critical instant.

Theorem 2.1: A critical instant for any task occurs whenever the task is requested simultaneously with requests for all higher priority tasks. Proof

2.2 Scheduling two Periodic Tasks

Given two tasks and with repetition periods T₁ and T₂ and execution times C₁ and C₂ . We shall attempt to define conditions so that they will be schedulable (i.e. terminate within their deadlines).

Assume, without loss of generality, that .

a. Assign higher priority than .

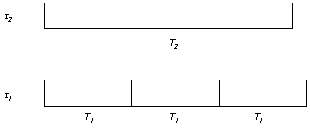
Figure 2.3

Then it is obvious that (in the worst case as required by Theorem 2.1) task must complete within T₁ and must leave enough time for task to complete before its deadline at . This can only happen if

              (2.1)

b. Assign higher priority than . Then, task will be preempted times during one period T₂ . Again, we consider the worst possible case as outlined previously when the two tasks and commence execution simultaneously.

Necessary and sufficient conditions for feasible scheduling are

             (2.2)

             (2.3)

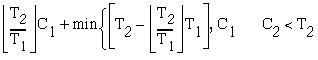             (2.4)

To explain relations (2.2),(2.3) and (2.4), refer to the following diagram

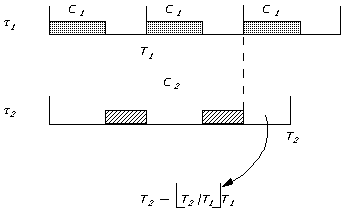
Figure 2.4

Since is of higher priority than , it will continuously pre-empt . During T₂, it will pre-empt times, and it will consume plus portion of the remaining time which is .

If is less than , then there will be some time left over for to run.

If then all the remaining time ( ) will be used by .

Therefore, the quantity gives the time, towards the end of , used by .

Observe now that if (2.1) is satisfied, then (2.4) is also satisfied. Indeed

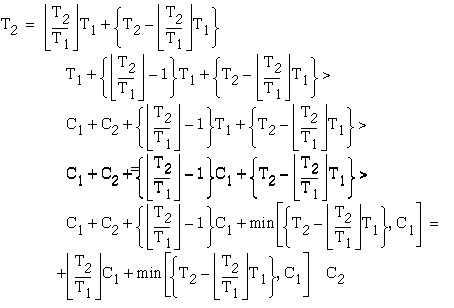        (2.5)

From the above, one observes that if (2.1) is true, no matter which schedule is followed (i.e., or [ signifies that task has lower priority than task ]) it is always possible for and to meet their deadlines.

On the other hand, if (2.4) is satisfied (which is a more general case, i.e., larger set of choices for and ) only f satisfies a feasible schedule.

We call this type of scheduling rate-monotonic scheduling .

It is also worth noting a necessary (but not sufficient) condition.

Given that tasks and are feasibly scheduled, then

           (2.6)

Observe now that from (2.1), we can also obtain (2.6) above as follows:

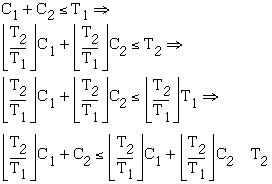               (2.7)

Theorem 2.2: If a feasible priority assignment exists for a set of tasks, the rate-monotonic priority assignment is feasible for that task set. Proof