Introduction
rate monotonic and the deadline driven scheduling were designed to guarantee the deadlines of periodic tasks.
A more realistic environment though, is one where both periodic and aperiodic tasks co-exist. Normally, in such an environment, the periodic tasks have hard deadlines and are used to serve instruments and/or control loops while the aperiodic tasks have soft deadlines, and are dedicated to user interaction.
Different criteria must be used in order to schedule such a tasking environment. While the rate-monotonic assignment or deadline driven scheduling succeed in the case of purely periodic and hard deadline environments, the uncertainty regarding the appearance of requests by the aperiodic tasks, makes these scheduling disciplines inapplicable in the presence of aperiodic tasks.
In addition, since the aperiodic tasks are primarily used for user interaction, one would like to optimize their response time in addition to meeting the hard deadlines of the periodic tasks.
Two alternatives have been developed:
Treat the aperiodic tasks in the background, filling in any processing gaps left by the set of periodic tasks. This approach guarantees the deadlines of the periodic tasks and maximizes the utilization factor of the processor but since it delegates the aperiodic tasks to the lowest possible priority, it favors long response times from these tasks.
Where shorter response times are required, the polling method is used. In this method a server task wakes up periodically and executes any waiting aperiodic task. The main problem with this method is that because of the bursty nature of the aperiodic tasks, the server often misses them by one period, and it may not have enough capacity to support a large burst.
The priority exchange and the deferrable server algorithms have been designed to overcome this time misalignment. Both algorithms utilize a periodic server, which is a task that handles the running of the aperiodic tasks. They differ as to when and how the periodic server is invoked, and how it (the periodic server) interacts with the aperiodic and periodic tasks.
3.1 The Priority Exchange Algorithm
This algorithm assigns the periodic server the highest
priority i.e. the periodic server has a period 
which is less than the period
of all the other periodic tasks.
The periodic server is assigned a certain run time C1 which it normally uses to service waiting aperiodic tasks.
Of course the total utilization factor should follow the Liu and Leyland limit for the rate monotonic scheduling i.e.
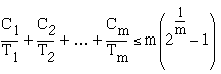
The scheduling of the periodic
server proceeds as follows:
At the start of its period, the periodic server is invoked, and services
any aperiodic tasks (if any) that are waiting. If after it finished servicing
the aperiodic tasks, there is still time remaining, then the aperiodic
server exchanges priority with the highest-priority waiting periodic task.
Thus, the periodic task is now serviced, while the periodic server preserves
the remainder of its run time for later on in case that a new aperiodic
task arrives. In such an event, the periodic server resumes its normally
high priority, pre-empts the periodic task and services the newly arrived
aperiodic task. If the periodic server has not exhausted its allotted
run time processing waiting aperiodic tasks, then a newly arriving aperiodic
task will be serviced immediately.
A caveat that we need to be aware of. The Priority Exchange Algorithm does not "bank" time. That is, the periodic server needs at least one waiting periodic task to exchange its priority with. If no periodic tasks are waiting, no exchange takes place, and the periodic server simply idles until the end of its run time, or until a periodic or aperiodic task arrives.
3.1.1 Conservation of Schedulability
Theorem
3.1: For a set of m fixed priority
periodic tasks 
where
is a periodic server that can trade run time with lower
priority tasks as per the discussion above, the schedulability of the
periodic task set 
is preserved. Proof
Theorem
3.2: For a set of m periodic tasks
scheduled using the rate monotonic algorithm, and if 
is the highest priority task, the least upper bound of the utilization
factor is given as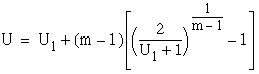 
.
Proof
If one plots U against U1, one would obtain
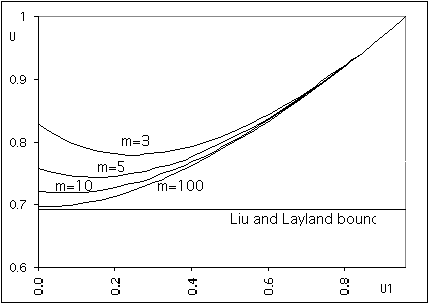
Figure 1: Least Upper Bounds of the processor Utilization for the Priority Exchange and the rate monotonic schedules.
Thus the schedulability threshold, depends on the utilization factor of the highest priority task (i.e. the periodic server). And it is higher than the 70% lower bound given for periodic tasks.
(Qualitatively speaking, the high priority server consumes
certain processor power. The remaining is distributed among the periodic
tasks for which the 70% Liu and Layland bound holds. The higher the U1
is, the better the overall utilization, but then 
, the periodic server, monopolizes
the processor).
3.2 The Deferrable Server (DS) Algorithm
The deferrable server is similar to the priority exchange in the sense that it allocates certain time for serving aperiodic tasks. In contrast to the PE. though, it does not trade priority with any lower priority periodic task, but it keeps its high priority (and hence the processor time) for the whole duration C1 of the execution time of the server.
The DS algorithm achieves a lower utilization bound for the set of periodic tasks, but at the same time it is easier to implement as compared to the PE. algorithm and thus has a lower overhead.
Also, the periodic server can start its execution any time within its period T1. Thus, it responds optimally to the arrival of aperiodic tasks. In addition, if any portion of C1 is left unused at the end of the repetition period T1, it is discarded.
The remainder of the periodic tasks follow Liu and Layland's [1] arrangement.
3.2.1 Worst Case Model
Since the periodic server can start at any time within its period, the worst case is when two successive C1 `s are requested, and also when all the periodic tasks are lined up at the onset of the first request. We shall prove that the worst fully utilized values of Ci are given as
.
.
.
(3.6)
First the schedule is feasible.
Indeed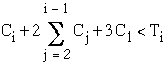 
To prove the above, we proceed as follows
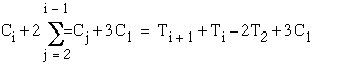
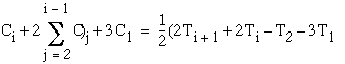(3.7)
Since 
then
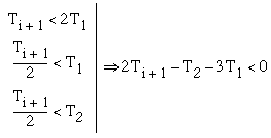(3.8)
From equations (3.7) and (3.8), one obtains
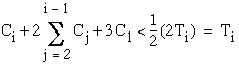
and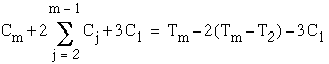 
Additionally, in a similar manner as the rate monotonic
case, this schedule fully utilizes the processor, and the run times are
chosen so as within one period there will be exactly two invocations of
all the higher priority tasks and three invocations of the deferrable
server. It is assumed that the start times are arranged so as to coincide
and to allow the deferrable server to execute twice. Consider for example
the first task 
. The termination of the third
invocation of 
, under the worst case model as depicted
in Figure 3.4, will be at
, i.e. it will coincide with the end of the period of task 
.
Figure 3.2: Tasks and run times for a set of periodic tasks and the deferrable scheduler (t1) attaining the minimum utilization factor.
We shall see that this set of tasks yields the worst processor
utilization. Focus in tasks 
and 
and assume that a small perturbation is applied to the run time of task
(the deferrable server) increasing or decreasing its run time. Correspondingly,
the run time of task 
must decrease (increase) to compensate for the change
in the run time of 
and assure full utilization of the processor. The run times of all the
other tasks remain the same. As we shall see, such perturbations always
increase the utilization proving thus that the set of tasks defined by
(3.6) yields the smallest utilization.
Let therefore the run time of 
increase by 
to 
. The run time of 
must decrease by a commensurate amount to ensure that the set of tasks
fully utilizes the processor.
As it can be verified with the help of Figure 3.4 
, while the run times of the other tasks remain unchanged.
Denote by 
and 
the utilization factors for the perturbed and unperturbed task sets respectively.
Then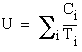 
and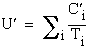 
. Comparing the utilization factors, we obtain
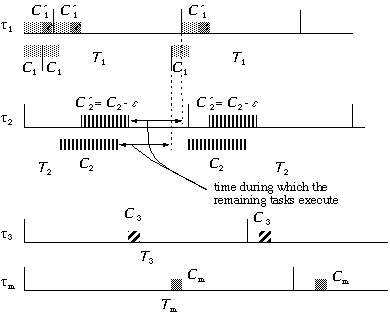
Figure 3.3: Perturbation
of the run time of the periodic server (
) and the resulting rearrangement of the run times of the remaining
tasks. Task (
) has its run time decreased. The original run times
for the first two tasks (
and 
) are depicted below the time lines. Observe that the
period of the periodic server has been shifted to the right by e
, which in conjunction with the decrease by e
to C2, does not alter the length of the time interval between the end
of C2 and the end of T1.It is within this time interval that the remaining
tasks execute, and since its length is not altered, these tasks have enough
time to complete within their deadlines.
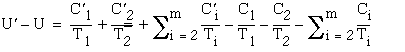
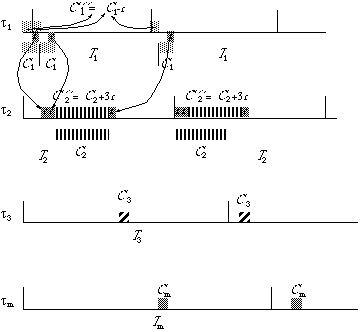
Figure
3.4: Perturbation of the run time of the deferable server (
) and the resulting rearrangement of the run times of the remaining
tasks. The reduction of the run time of the deferable server to 
results in idle intervals of total duration of 3 e which are utilized by task (
). The original run times for the first two tasks (
and 
) are depicted below the time lines.
Similarly, if the run time of 
decreases by e
, to 
, the run time of 
must increase by 3 e to 
to guarantee a fully utilizing the processor schedule (see Figure 3.4).
The run times of all other tasks remain unchanged.
Denote by 
and 
the utilization factors for the perturbed and unperturbed task sets respectively.
Then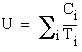 
and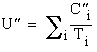 
. Comparing the utilization factors, we obtain
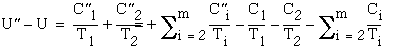
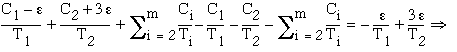
Thus, as it can be seen from (3.9) and (3.10), any perturbation
to the length of the run time of the deferrable server from 
results to a set of tasks that fully utilizes the processor and
has a higher utilization factor as compared to the unperturbed case.
Perturbations to the lengths of the run times of the other tasks are handled in the same way as for the case of the deadline driven scheduling, and they also results in sets of tasks with higher utilization factors.